Numbers can be classified in many ways. One way is to use a natural "gradation" from the more concrete to the more abstract types. For example:

• Natural numbers. These are the first numbers used by mankind. They are simply 1, 2, 3, and so on. These values were created as mental abstraction that could be used to count items.
• Cardinal numbers. These are merely the natural numbers plus 0 (zero). The concept of zero as a number was once puzzling to some, and it had no representation in roman numerals. Since it stands for "nothing" then why even talk about it? Of course it came to be accepted as an actual number.
• Integers. These are cardinal numbers to which a negative sign can be added to represent values smaller than zero. This concept of "less than nothing" was also initially considered unreasonable, and the term "negative" was coined on behalf of those who rejected it.
• Real numbers. These are integers to which a fractional part (or an additional value shown after a decimal mark) is added to represent portions of a whole. Here again, "less than a complete item" can be seen as a foreign concept in some context. But all modern-day students understand the usefulness of real numbers.
• Complex numbers. These are pairs of real numbers handled as a single unit. One of the two components is simply called "real". The other is called "imaginary" due to the fact that it represents a factor of the square root of -1, a value that cannot be represented using a simple real number. But both components of complex numbers are equally real, and complex numbers play a vital role in modern mathematics.

To represent a complex number with AddUp, parentheses are used to hold a list of two real numbers (a pair). The so-called "real" component is first in the list; the so-called "imaginary" component is second. A semi-colon separates both items in the list. For example, complex number "(1; 2)" has a real component with a value of 1 and an imaginary component with a value of 2.

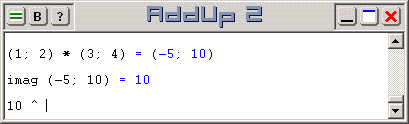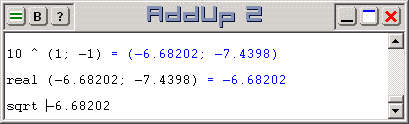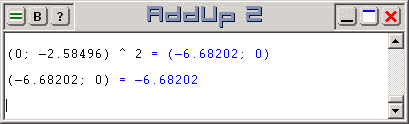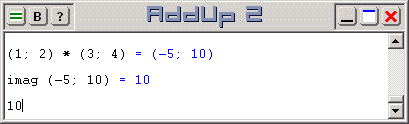
Operations on complex numbers are done with AddUp in exactly the same way as operations on real numbers. The complex number is simple entered wherever a real number could also be used. For example, multiplying two complex numbers is done with an expression such as "(1; 2) * (3; 4)".

A set of complex number functions is implemented in AddUp to explicitly take advantage of these values. They are:

• arg: Returns the argument (or phase angle) of a complex number.
• conj: Returns the complex conjugate of a complex number.
• imag: Returns the imaginary component of a complex number.
• norm: Returns the norm (or absolute value, or magnitude) of a complex number.
• norm2: Returns the square of the norm of a complex number.
• polar: Returns a complex number equivalent to the specified polar representation.
• real: Returns the real component of a complex number.